Les probabilités à la roulette
Le jeu de la roulette a été introduit à Paris vers 1760 par Sartines, lieutenant de Police, pour moraliser les jeux de hasard. La roulette proprement dite où sort le numéro gagnant est composé de deux parties : une partie fixe (la carcasse) et une partie mobile (le cylindre) qui s'encastre dans la carcasse. La carcasse comporte un axe central vertical et dans sa partie supérieure une piste tronconique agrémentée d'obstacles métalliques incrustés. Le cylindre est un disque comportant 37 cases à sa périphérie qui tourne sur l'axe de la carcasse et dont la circonférence affleure au bas de la piste tronconique de la carcasse. Dans les casinos on contrôle régulièrement à l'aide de niveaux l'horizontalité de l'ensemble.
Un coup de roulette consiste à faire tourner le cylindre dans un sens et à lancer une bille (en principe en ivoire) en sens inverse sur la partie tronconique de la carcasse. La symétrie, l'équilibrage du système, les mouvements inverses de la bille et du cylindre, les obstacles font que la roulette est une bonne machine « à fabriquer du hasard », en ce sens qu'il est pratiquement impossible de prévoir le mouvement de la bille et qu'aucune case du cylindre n'est favorisée. Les cases des cylindres sont numérotées de 0 à 36.
Ces numéros ont, à l'exception du zéro, trois caractéristiques :
1) Un numéro est MANQUE s'il est inférieur à 19 et PASSE dans le cas contraire.
2) Un numéro est PAIR ou IMPAIR (attention à la roulette le zéro n'est ni pair ni impair).
3) Un numéro est ROUGE ou NOIR de façon purement conventionnelle.
Un moyen simple de retrouver la couleur d'un numéro est d'utiliser la règle suivante : si la somme des chiffres du numéro est impaire modulo 9 (le reste après division par 9) il est ROUGE à deux exceptions près, le 10 et le 28 qui sont NOIR. Si cette somme est paire les numéros sont NOIRS sans exception.
Analyse du jeu
Maintenant si l'on examine la répartition des numéros sur la roulette, on s'aperçoit immédiatement qu'ils ont été disposés de façon à satisfaire plusieurs critères. Premièrement deux numéros consécutifs ne sont jamais voisins. Deuxièmement un NOIR est toujours entre deux ROUGE. Troisièmement deux numéros MANQUE ne sont jamais voisins (sauf le 5 et le 10), de même que pour les numéros PASSE, cela sans exception. Enfin, les numéros PAIR et IMPAIR alternent mais seulement 21 fois sur 35.
Il y a mieux : si l'on considère le zéro comme le Nord, le cylindre peut être divisé en deux groupes de 18 numéros en Est et Ouest, dont la somme est égale à 333, ce qui n'est pas dû au hasard et traduit bien le souci d' « équilibrage » des créateurs de la roulette. Cette disposition a-t-elle une importance ? Non dans la mesure où mécaniquement, la roulette est bien conçue et même une répartition en moitié ROUGE et moitié NOIRE ne changerait rien au caractère aléatoire de la roulette idéale. Toutefois si quelques défauts minimes d'équilibrage ou de rugosité favorisaient une portion du cylindre, cette disposition en atténue les effets.
Passons à la table de mise. Ce tableau d'apparence complexe permet une grande diversité de jeux, ce qui explique la faveur de la roulette comparé à la boule (roulette à neuf numéros).
Types de mise |
Nombre de numéros |
Gains |
|
Chances simples |
Noir |
18 |
1 |
Rouge |
18 |
1 |
|
Impair |
18 |
1 |
|
Pair |
18 |
1 |
|
Passe |
18 |
1 |
|
Manque |
18 |
1 |
|
Chances multiples |
Le plein |
1 |
35 |
Le cheval |
2 |
17 |
|
La transversale |
3 |
11 |
|
Le carré |
4 |
8 |
|
Le sixain |
6 |
5 |
|
La douzaine ou la colonne |
12 |
2 |
|
24 numéros |
24 |
1/2 |
> Voir le placement des mises sur le tapis de la roulette
Voyons les différents jeux possibles avec une seule mise. On a d'abord les chances dites simples : ROUGE, NOIR, PAIR, IMPAIR, PASSE et MANQUE, Où l'on joue sur 18 numéros et où l'on gagne deux fois la mise. Ensuite il y a les chances multiples qui sont le numéro plein pour lequel on place sa mise sur un seul numéro, le cheval pour lequel on met sa mise à cheval sur deux numéros, la transversale pleine pour laquelle on mise sur le bord d'une bande de trois numéros horizontaux, le carré que l'on joue en plaçant sa mise à l'intersection commune à quatre numéros, la transversale simple (ou sixain) où l'on pose sa mise sur le point commun de deux bandes de trois numéros horizontaux. Enfin, on peut miser sur 12 numéros soit en colonne, soit de 1 à 11, 18 à 24 et 25 à 36 en utilisant les cases du bas de la table de mise. On peut aussi jouer 24 numéros en mettant sa mise à cheval sur les cases de jeux à 12 numéros.
Remarquons que bien que les possibilités soient grandes, tous les jeux envisageables avec une seule mise ne sont pas possibles. Ainsi pour les chevaux il y a 36 X 37 = 1332 chevaux envisageables mais seulement 60 jouables effectivement avec une seule mise. Il reste néanmoins 161 formes de jeu avec une seule mise.
À chaque coup de roulette ou « boule » le croupier annonce le numéro gagnant ainsi que les chances simples gagnantes comme par exemple : 1, NOIR, IMPAIR et MANQUE et les gains sont attribués selon le tableau précédent pour les chances multiples.
Dans la pratique le croupier ne paie que le complément à la mise qui est sur le tapis, c'est-à-dire que sur un numéro le croupier paie 35 mises et le joueur peut récupérer sa mise sur le tapis ce que des joueurs novices oublient parfois de faire. Remarquons que sur 24 numéros le paiement étant 1,5 fois la mise, il faut nécessairement jouer deux mises minimales pour pouvoir être payé (il existe une mise minimale). Pour les chances simples la sortie du zéro a des conséquences particulières sur lesquelles nous reviendrons plus loin.
L’espérance mathématique de gain
La première question que l'on devrait se poser lorsque l'on joue à un jeu de hasard est : quelle est l'espérance (mathématique) de gain, c'est-à-dire quel est le produit du gain éventuel par la probabilité qu'il a de se réaliser ? Si, pour une mise de un euro, cette espérance vaut 1 le jeu est équitable, si elle est plus grande que 1, le joueur est avantagé, si elle est inférieure à 1, c'est la maison de jeux qui est avantagée.
Prenons le cas du jeu sur un numéro de roulette. Si l'on gagne on touche 36 euros mais l'on a une chance sur 37 de gagner d'où l'espérance mathématique 36/37. L'écart à 1, ici 1/37, correspond à « l'impôt du jeu » ou à la cagnotte du casino, soit 2,7 pour cent de la mise. Une autre façon d'évaluer cet impôt est d'imaginer un joueur qui « pour voir » miserait un euro sur tous les numéros. De cette façon il est certain de gagner quelque chose mais calculons son bilan après le coup : il a mis 37 francs sur le tapis, on lui a payé 36 francs, il perd un franc, soit 1/37 de sa mise totale.
Cet impôt varie-t-il selon le choix de la chance multiple jouée ? Non ! Pour se convaincre que l'impôt est constant prenons l'exemple du jeu sur un carré : on touche neuf fois la mise mais l'on a 4/37 chances de gagner d'où l'espérance mathématique 4/37 X 9 = 36/37, identique à celle du jeu sur un numéro.
Examinons maintenant le cas des chances simples. Là, il y a une particularité : si le zéro sort, les chances simples sont mises « en prison », c'est-à-dire que les mises sont laissées sur le tapis et reportées à la boule suivante (on peut néanmoins modifier son jeu sur les chances simples pour la boule suivante). À la boule suivante si la chance simple gagne le joueur peut reprendre sa mise mais sans être payé et dans le cas contraire c'est le casino qui ramasse la mise. Si le zéro sort deux fois de suite, les mises seront emprisonnées pour deux boules : elles ne seront récupérables que si l'on gagne deux fois de suite. Sur la table de mise, il n'est prévu que trois emprisonnements car il est vrai qu'une suite de quatre zéros est très rare.
Quelle est l'espérance mathématique du jeu sur une chance simple ? Pour simplifier nous supposerons que le zéro ne sort pas deux fois de suite, ce qui ne se produit qu'une fois sur 37 X 37, soit 1369, et l'erreur ainsi commise est minime. Au premier coup on a 18 chances sur 37 de gagner deux mises et si le zéro sort (1 chance sur 37) une chance sur deux (car l'on a supposé que le zéro ne sort pas deux fois de suite) de récupérer sa mise d'où l'espérance mathématique : E= 18/37 X 2 + 1 X 1/37 X 1/2 = 73/74, c'est-à-dire que, dans ce cas, l'impôt du jeu est 1/74 = 1,35 pour cent, soit deux fois moins que sur les chances multiples.
Attention il ne faut pas immédiatement en conclure qu'il est plus intéressant de jouer sur les chances simples... mais plutôt que l'intérêt du casino est que les joueurs jouent les chances multiples.
Comment évoluent nos chances de gagner au cours d'un certain nombre de parties ? Si je joue un coup sur un numéro, j'ai 36/37 chances de ne pas gagner. Maintenant si je joue deux coups, j'ai 36/37 chances de ne pas gagner au premier coup et toujours 36/37 chances de ne pas gagner au deuxième coup. Donc ma probabilité de ne pas gagner en deux coups est (36/37)2, évidemment plus faible. Plus généralement si je joue n parties j'ai (36/37)n chances de ne pas gagner du tout donc 1 - (36/37)n de gagner au moins une fois. Ce raisonnement peut être tenu pour toutes les autres chances multiples (en modifiant les probabilités en conséquence) aussi est-il intéressant de représenter graphiquement ces résultats comme illustrés ci-dessous.
Probabilité de gagner au moins une fois sur les différentes chances de la roulette en n coups :
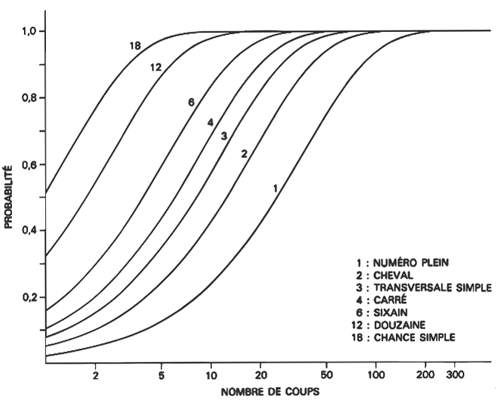
Ce graphique appelle quelques remarques : pour avoir une chance sur deux de gagner au moins une fois sur un numéro il faut jouer 25 parties en moyenne. Si l'on veut une quasi-certitude de gagner au moins une fois sur un numéro (c'est-à-dire à 99 chances sur 100), il faut jouer 170 coups, c'est-à-dire risquer 170 euros pour en gagner sûrement 36 ! Si l'on est moins téméraire, en jouant sur un sixain on sera « récompensé » plus vite, en ce sens qu'il faut quatre coups en moyenne pour avoir une chance sur deux de gagner au moins une fois et 26 coups pour s'assurer une quasi-certitude, mais naturellement les gains (comme les pertes) seront plus faibles. Tous ces calculs donnent la probabilité de gagner au moins une fois mais englobent aussi les probabilités de gagner une fois, deux fois, etc.
Comment modifier ces calculs pour obtenir la probabilité de gagner k fois exactement en n parties ? Désignons par p la probabilité de gagner sur une partie et q, égal à 1 - p, la probabilité de perdre. Commençons par la probabilité de gagner une fois exactement en n parties. Pour cela il faut gagner une fois, (probabilité p) et perdre n - 1 fois (probabilité qn-1) donc la probabilité est pqn-1 mais le gain peut se produire au premier coup, au deuxième coup, etc., c'est-à-dire de n façons différentes, d'où la probabilité npqn-1. De même pour gagner deux fois exactement en n coups la probabilité de 2 gains et de n - 2 pertes est p2qn-2 mais il y a C2n= n(n-1)/2 façons de le réaliser (c'est-à-dire le nombre de façons de choisir les deux coups gagnants parmi les n coups joués) soit en définitive une probabilité C2np2qn-2. Plus généralement la probabilité pour gagner k fois exactement sur n coups est : Pk = Cknpkqn-k
La figure suivante montre l'évolution de cette probabilité dans le jeu sur un numéro (p = 1/37) pour k = 1, 2, 3 et 4.
Probabilité de gagner exactement 1, 2, 3, ou 4 fois sur un numéro plein à la roulette :
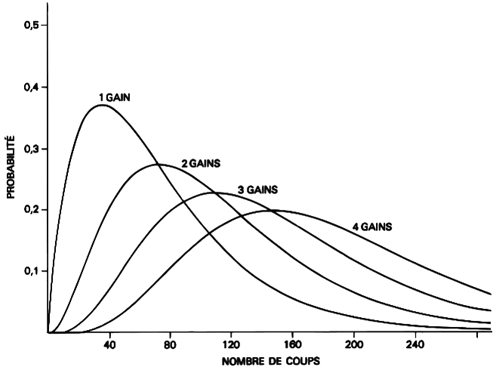
Remarquez que toutes ces courbes commencent par croître puis passent par un maximum, ce qui se comprend fort bien car plus le nombre de parties augmente plus la chance de gagner plusieurs fois augmente et corrélativement celle de gagner un nombre de fois plus petit diminue.
Munis de la formule précédente nous sommes à même d'étudier l'avenir du joueur de fond qui joue toujours la même mise sans rater une partie. Quelle est sa probabilité d'être gagnant au bout de 2n parties s'il joue sur les chances simples ? Dans le cas présent nous ne tiendrons pas compte de la particularité du zéro en admettant que, lorsqu'il sort, le joueur perd sur les chances simples, ce qui ne change pas le résultat que l'on cherche. Sa probabilité p de gains à chaque coup est 18/37. Pour que le joueur soit perdant au bout de 2n coups il faut et il suffit qu'il n'ait pas gagné plus de n-1 fois mais la probabilité pour qu'il n'ait pas gagné plus de n-1 fois est la somme des probabilités pour qu'il ait gagné zéro fois, une fois, deux fois, etc. n-1 fois, c'est-à-dire d'après la formule précédente :
P = ∑n-1k=0 Ck2n pk q2n-k
Dès que n est un peu grand, le calcul de cette somme est un travail de titan, c'est pourquoi les mathématiciens du XVIIIe siècle (en particulier Stirling) ont construit des formules approchées permettant d'évaluer cette somme. Ces formules sortent du cadre de cet article et je n'indiquerai que le résultat résumé dans le tableau ci-dessous.
Probabilité de perdre aux chances simples :
Nombre de coups joués |
Probabilité de perdre aux chances simples |
1 |
0,514 |
50 |
0,520 |
100 |
0,568 |
500 |
0,698 |
2 500 |
0,903 |
7 500 |
0,989 |
15 000 |
0,992 |
20 000 |
0,999 |
À la lecture de ce tableau on voit immédiatement que sur 500 coups on a déjà presque trois chances sur quatre d'être perdant et que plus le nombre de partie augmente, plus la probabilité de perdre se rapproche inexorablement de 1 : c'est un des aspects du phénomène de la ruine du joueur sur lequel nous reviendrons plus loin. Nous aurions pu aussi faire le raisonnement pour le jeu sur une chance pleine et, dans ce cas, on montre que la probabilité de perdre commence par diminuer puis passe par un minimum et puis tend vers 1, mais beaucoup plus lentement, ce que nous montrerons d'une façon différente un peu plus loin.
Abandonnons les perdants pour nous intéresser uniquement aux chanceux. Sur 2n parties de chance simple les chanceux seront ceux qui ont gagné n + 1, n + 2, ... n + k... 2n fois.
Appelons « chance normale » le nombre k tel que la moitié des joueurs chanceux ont gagné plus et par conséquent la moitié a gagné moins. Calculons ce nombre. Il y a Cn+12n façons de gagner n + 1 fois, Cn+22n de gagner n + 2 fois... donc au total : ∑n+ki=n+1 Ci2n façons d'être chanceux. D'autre part le nombre de façons qu'un joueur chanceux a de gagner au plus n + k fois est : ∑n+ki=n+1 Ci2n
La probabilité d'avoir gagné au plus n + k fois est le rapport de ces deux sommes et la valeur que l'on cherche est le nombre k tel que cette probabilité soit égale à 0,5. Là encore nous n'indiquerons que les résultats dans le tableau ci-dessous :
Nombre de coups joués |
Chance normale |
200 |
8 |
800 |
16 |
3200 |
32 |
6400 |
64 |
Ainsi sur 200 parties de chances simples un gain de huit mises correspond à une chance normale et inversement une perte de huit mises serait une « guigne normale ». Ce qu'il y a de plus intéressant dans ce tableau c'est que la chance normale croît avec le nombre de parties mais seulement comme la racine carrée du nombre de parties jouées, ce qui ne récompense guère l'obstination, d'autant plus qu'il faut toujours faire partie des chanceux ! De plus nous n'avons pas tenu compte de l'impôt du jeu résultant de la sortie du zéro en moyenne tous les 37 coups qui « absorbe » une mise en moyenne tous les 74 coups. Ainsi à partir de 3100 coups l'impôt du jeu (43 mises) a déjà dépassé la « chance normale ».
Réduire les pertes
Maintenant que nous savons que si l'on joue longtemps il faut se résoudre à perdre, peut-on retarder sa perte selon sa façon de jouer ? Pour cela examinons les deux cas extrêmes d'un groupe de joueurs qui jouent une mise sur les chances simples et un autre groupe de joueurs qui mise sur un numéro plein. La probabilité de gagner k fois en n parties est nous l'avons vu Cknpkqn-k avec p = 18/37 pour les chances simples et p = 1/37 pour le numéro plein. La probabilité de gagner i fois au plus est P = ∑ik=0 Ckn pk qn-k. Connaissant n, p et q on peut calculer les nombre i1 et i2 tels que p soit égal à 0,25 ou 0,75.
Pour nos groupes de joueurs les nombres i1 et i2 seront le nombre de parties gagnées par au moins 75 pour cent des joueurs et au plus par 25 pour cent des joueurs. Cela veut dire que le bilan de 50 pour cent des joueurs sera compris entre n - Ri1 et n - Ri2 mises si R est le gain du jeu choisi (2 pour les chances simples et 36 sur le numéro plein). Les résultats du calcul sont ceux du tableau ci-dessous :
Après |
Bilan de 50 pour cent des joueurs |
|
Chance simple |
Numéro plein |
|
100 coups |
entre - 10 et + 4 |
entre - 28 et + 44 |
500 coups |
entre - 28 et + 2 |
entre - 104 et +76 |
1 000 coups |
entre- 48 et - 6 |
entre - 136 et + 80 |
2 000 coups |
entre - 84 et - 24 |
entre - 236 et + 124 |
10 000 coups |
entre - 338 et - 202 |
entre - 676 et + 116 |
20 000 coups |
entre - 636 et - 446 |
entre - 1 100 et + 16 |
25 000 coups |
entre - 782 et - 570 |
entre - 1312 et - 62 |
Pour une suite de n coups avec la même mise, 50 pour cent des joueurs auront un bilan compris entre les deux nombres indiqués.
La lecture de ce tableau est simple. Prenons par exemple 1000 coups, le tableau indique qu'un quart des joueurs sur un numéro plein auront perdu plus de 136 mises, une moitié aura entre 136 mises de pertes et 80 mises de gain et enfin un quart gagnera plus de 80 mises. On voit immédiatement sur ce tableau que si, sur les chances simples entre 500 et 1000 coups, trois quarts des joueurs seront perdants, sur un numéro plein trois quarts des joueurs ne seront perdants que vers les 20 000 coups, c'est-à-dire qu'en jouant sur un numéro plein on peut avoir un bilan positif plus longtemps que sur les chances simples mais naturellement au risque aussi d'avoir des pertes plus importantes ! Bien sûr les autres façons de jouer cheval, carré, etc. se situent entre ces deux extrêmes. Revenons sur la mise des joueurs que nous avons mise en évidence pour un joueur qui ne raterait pas une partie et qui jouerait la même mise à chaque coup. (Le fait que le jeu ne soit pas équitable n'a pas réellement d'influence théorique : quand le jeu est équitable (p = q = 1/2) le joueur se ruine moins vite et c'est tout.) Si le joueur choisit les moments où il joue (en suivant une martingale par exemple) et la mise qu'il va jouer, le problème de la ruine est beaucoup plus difficile à mettre en forme et à résoudre. Ce n'est qu'au XXe siècle sous l'impulsion de mathématiciens comme J.L. Doob et J. Ville qu'il a pu être résolu. Au XIXe siècle ce résultat était considéré comme une vérité d'évidence au même titre que l'impossibilité du mouvement perpétuel. La non-existence d'une martingale (façon de jouer toujours gagnante) est, en quelque sorte, une condition nécessaire de l'existence du hasard.